Before reading this page, it will help to have read ‘Resolving the 5th Chord‘.
Take any major chord and make it a dominant 7th. For simplicity we will start with one that uses only white notes, C major.
C – E – G
To make it a C7 we add a note that is two half steps (frets) below the root – i.e. Bb
C – E – G – Bb
Now resolve this chord by moving the 3rd of the chord half a step higher (E -> F) and the 7th of the chord half a stope lower (Bb -> A).
Now play the chord, leaving out the 5th of the original chord. We have C, F and A, which are the notes of the chord of F major (F – A – C).
So we have gone through the following steps;
- Major chord (C)
- Make it a 7th (C7)
- Resolve by lifting the second and lowering the 7th (E->F, Bb > A)
- Play result (F)
Now repeat this process with the F chord
- F -> F7 -> Bb
If we keep going we get the following sequence (including the first two changes)
- C -> C7 -> F
- F -> F7 -> Bb
- Bb -> Bb7 -> Eb
- Eb -> Eb7 ->Ab
- Ab ->Ab7 ->Db
- Db ->Db7 ->Gb (which is also the same as F#)
- F# -> F#7 -> B
- B -> B7 -> E
- E -> E7 -> A
- A -> A7 -> D
- D -> D7 -> G
- G -> G7 -> C
And suddenly, we are back wher we started. We have gone round in a circle, by continually making a chord a 7th, and resolving it. Each chord that modify becomes the chord V (five) in the key that we end up in (e.g. G becomes G7, which is chord 5 in the key of C). THis sequence is therefore known as the Circle of 5ths, and is often shown like this.
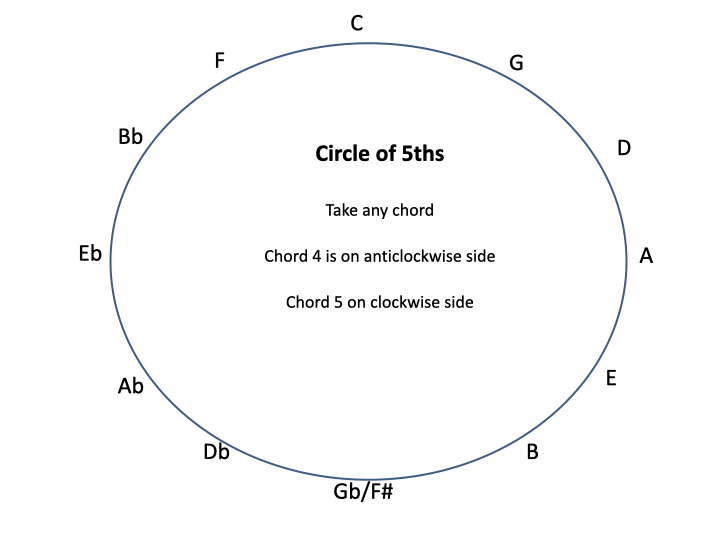
There are several intreseting things about this circle
At any starting point, chord 4 is on the anticlockwise side and chord 5 is onthe clockwise side
- At any starting point, chord 4 is on the anticlockwise side and chord 5 is on the clockwise side (e.g. F to the left of C, G to the right).
- If C is at the top, which has no sharps or flats, then the next key going clockwise has one sharp (G, the next has 2 (D) and so on. So you can instantly work out how many sharps there are in a key, using the clockwise side.
- With C at the top, and going anti-clockwise, the first key has one flat (F), the next has 2 flats (Bb) and so on.
There are further patterns that emerge from this wheel. Taking the sharp keys;
- Key of G has one sharp (F#) and the F is 2 steps further back.
- Key of D has 2 sharps, which are C and F (which are 2 and 3 steps back)
- Key of A has three sharps which are G, C and F (which are 2, 3 and 4 steps back).
- and so on until maximum of 7 sharps reached (key of G#)
A similar pattern emerges for the flat keys
- F has one flat (Bb) which is 2 steps anti-clockwise from the top
- Bb has 2 flats (Bb and Eb), which are 2 and 3 steps anti-clockwise from the top
- Eb has 3 flats (Bb, Eb and Ab), which are 2,3 and a steps anti-clockwise from the top
- and so on until maximum of 7 flats reached (key of Cb)